Play with team M53 fir Greyctf last weekend, nice ctf got easy to hard challenges, and we got 56th place overall!
Here are some writeups of the challenges I solved
Challenges
EncryptService
Description
Attachment
After analyzed the source code, we can see it is using AES CTR mode to encrypt the flag:
def encrypt(plaintext, iv):
hsh = sha256(iv).digest()[:8]
cipher = AES.new(secret_key, AES.MODE_CTR, nonce=hsh)
ciphertext = cipher.encrypt(plaintext)
return ciphertext.hex()
...
...
print("Flag: ", encrypt(FLAG.encode("ascii"), os.urandom(1)))
Also we are given ciphertext with 256 different nonce:
for i in range(256):
ciphertext = encrypt(plaintext, i.to_bytes(1, 'big'))
print(f"Ciphertext {i}: {ciphertext}")
Analyse
Look at the wikipedia page of AES CTR mode, we can clearly see the encrypt and decrypt process:
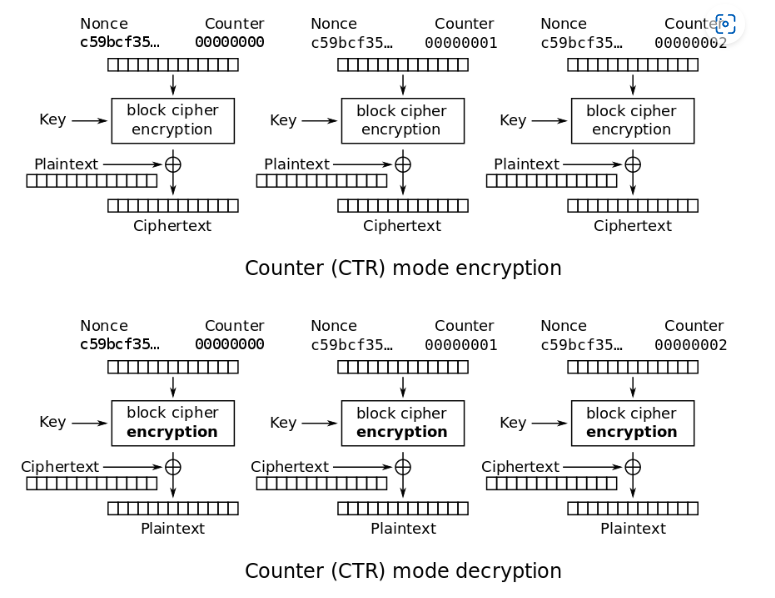
Notice the encrypt and decrypt process are the same! It just XOR the plaintext/ciphertext with the AES encryption
And we are given ciphertext for all possible nonce, so we can just XOR all 256 ciphertext with the encrypted flag and see which return the flag format!
Solution
My solution in python script:
from pwn import *
ciphertext = []
p = remote("34.124.157.94" ,10590)
# Send 40 null bytes (flag is 40 characters long)
p.sendlineafter(": ","00"*40)
for i in range(256):
p.recvuntil(": ")
ciphertext.append(p.recvuntil('\n')[:-1])
p.recvuntil("Flag: ")
flag = p.recvuntil('\n')[:-1]
# XOR all ciphertext with the encrypted flag
for c in ciphertext:
f = xor(bytes.fromhex(c.decode()),bytes.fromhex(flag.decode()))
if f.startswith(b"grey{"):
print(f)
# b'grey{0h_m4n_57r34m_c1ph3r_n07_50_53cur3}'
Flag
grey{0h_m4n_57r34m_c1ph3r_n07_50_53cur3}
GreyCat Trial
Description
Attachment
We are given a python script, we need to pass 3 trials to get the flag
We need to input 2 numbers:
a = int(input("The first element: "))
b = int(input("The second element: "))
all_seeing_number = 23456789
First Trial
# FIRST TRIAL
if b <= 0:
print("Verily, those who would cheat possess not the might of true wizards.")
exit(0)
if pow(all_seeing_number, a - 1, a) != 1:
print("Alas, thy weakness hath led to defeat in the very first trial.")
exit(0)
As you can see, we need to input the a value to satisfy the equation \(23456789^{a-1} \equiv 1 \mod a\)
If you’re familiar with math, you will notice this is Fermat’s little theorem:
\[a^{p-1} \equiv 1 \mod p\]
It means any prime number will satisfy the equation above, so we just input a prime number will pass the first test!
Second Trial
# SECOND TRIAL
trial_numbers = [randint(0, 26) for i in range(26)]
for number in trial_numbers:
c = a + b * number
if pow(all_seeing_number, c - 1, c) != 1:
print("Thou art not yet strong enough, and thus hast been vanquished in the second trial")
exit(0)
This was hard to satisfy, because the trial_number is 0 to 26 random pick 26 numbers, and the value c has to be prime number?
Well after I read the wikipedia for Fermat’s little theorem notice pseudoprime/Carmichael number will also satisfy the equation
Then I look at the wiki of Carmicheal number stated:
Thomas Wright proved that if \(a\) and \(m\) are relatively prime, then there are infinitely many Carmichael numbers in the arithmetic progression \(a+k \cdot m\), where \(k=1,2,...\)
Which was quite similar for the second trial \(a+b \cdot n\), but I cannot find any example for this statement..
Closest I found was this article, but I tested the success rate is low (we need to satisfy 26 times for trial numbers)
Solving
So I just solve it by bruce forcing the value of \(a\) and \(b\), we know \(a\) must be prime so I copy the first 1-1000 prime numbers and brute force it with python script:
for b in range(1, 1000):
for a in [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509, 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673, 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853, 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997]:
count = 0
for i in range(27):
c = a + b * i
if pow(23456789,c-1,c) == 1:
count += 1
if count > 20:
print(a,b)
print(count)
# 3 2
# 22
# 5 2
# 21
# 7 2
# 21
# 11 2
# 21
# 13 2
# 21
From the result we can see the higest success rate is 3 and 2, so I made a while true loop to keep sending 3\n2 until it return the flag!
while true;do echo -e "3\n2" | nc 34.124.157.94 10592| grep grey;done
# grey{Gr33N-tA0_The0ReM_w1z4rd}
Flag
grey{Gr33N-tA0_The0ReM_w1z4rd}
Intended Solution
The original solution is actually using Green-Tao theorm, the writeup in github
OT
Description
Attachment
After reading the code, we can see it implements RSA encryption and we need to provide the modulus \(N\):
print("This is my new Oblivious transfer protocol built on top of the crypto primitive (factorisation is hard)\n")
print("You should first generate a number h which you know the factorisation,\n")
print("If you wish to know the first part of the key, send me h")
print(f"If you wish to know the second part of the key, send me h - {23}\n")
N = int(input(("Now what's your number: ")))
check = checkN(N)
if check != None:
print(check)
exit(0)
k1, k2 = secrets.randbelow(N), secrets.randbelow(N)
k = k1 ^ k2
Also to ensure we only can decrypt one part of the key k, it adds 23 to our modulus for k2 encryption:
print("Now I send you these 2 numbers\n")
print(f"pow(k1, e, N) = {pow(k1, e, N)}")
print(f"pow(k2, e, N+23) = {pow(k2, e, N + 23)}\n")
Then it provides the XOR encrypted flag, we must know the value of k to decrypt the flag!
print("Since you only know how to factorise one of them, you can only get one part of the data :D\n")
print("This protocol is secure so sending this should not have any problem")
print(f"flag = {encrypt(k, FLAG).hex()}")
print("Bye bye!")
So how we know k if we cannot decrypt both k1 and k2 ?
RSA
At first I though this was easy, just generate 2 prime numbers (like typical RSA \(N=pq\)) then factorize the factors of the 2 prime numbers + 23 : \(pq+23\), then can calculate the private key d
The problem is the number is very diffcult to factorize, because is a large number (4096bits), and we don’t know it contain what factors
First attempt
Then I thinking we can find 2 prime numbers which their difference is 23. Ex: \(p-q=23\) so we can calculate the phi and d easily.
But notice the code got do some check for modulus:
def checkN(N):
if (N < 0):
return "what?"
if (N.bit_length() != 4096):
return "N should be 4096 bits"
if (isPrime(N) or isPrime(N + 23)):
return "Hey no cheating"
return None
So I guess need to find other way
Second attempt
As we know 23 is a prime number, then I think we can generate a prime number p and times 23, so we submit \(23(p-1)\) as the modulus.
Therefore, \(N_1=23(p-1)\) and \(N_2=N_1+23=23p\)
But we still need to factorize p-1, then I remember a type of number which is vulnerable to Pollard’s p-1 algorithm
Which is a prime that is a smooth number plus one
Luckily I remember TJCTF previously got the generate script for that:
small_primes = [n for n in range(2,10000) if isPrime(n)]
def gen_smooth(N):
r = 2
while True:
p = random.choice(small_primes)
if (r * p).bit_length() > N:
return r
r *= p
p = 1
while not isPrime(p):
p = gen_smooth(1024) + 1
q = getPrime(1024)
n = p * q
Then I wrote a script to generate a 4091bits smooth number + 1 and is prime number, then times 23 (23 is 5bits so total will be 4096bits)
from Crypto.Util.number import isPrime
import random
small_primes = [n for n in range(2,10000) if isPrime(n)]
def gen_smooth(N):
r = 2
while True:
p = random.choice(small_primes)
if (r * p).bit_length() > N:
return r
r *= p
p = 1
# not sure why I need to put 4092 in order to get the correct bit length
while not isPrime(p) or p.bit_length() != 4092:
p = gen_smooth(4092)+1
q = 23
n = p*q
print(f"{p=}")
print(f"{n.bit_length()}")
print(f"{n=}")
# p=45043706549320376764699240869105281319861307456527546739259818058221306119685101489460914479194089897038717190836464418380678171709678542641613020291993545440696409912542830029917124966590818971097377090072166890548106908370393486645223411337596490056729440182703916234325126664410061697265111211935031091042505209336336461173210167404999043514950575263831206188618796903336901184165178509756924546538456248094370763593985143998644944671323092770975344948802678372748566330458297430162152966358168065645502861312698561370349134494362630362795348627099640197493406656270982866963600028027614404894525614592191551951417557936393217008016391473662540653824005772755285477032979052188647873621522448526925841240993058340627450063674093561196617003780253850906988729802863258092798579540539550480884627699899005284760430139399889142859405700333699803119281056922601393368451320117892966653270588206856589138124279402105546448509048228141075606675530361004482464493264651584150092177582461758039608666228004271909059532671504686565077158934235373549611219997703452839654370165935122675702192052601786026319921590474119711745445765501392393328698895310032072422053879021478924222918967534991609224082738990769172143931722530464727758002103
# 4096
# n=1036005250634368665588082539989421470356810071500133575002975815339090040752757334257601033021464067631890495389238681622755597949322606480757099466715851545136017427988485090688093874231588836335239673071659838482606458892519050192840138460764719271304777124202190073389477913281431419037097557874505715093977619814735738606983833850314978000843863231068117742338232328776748727235799105724409264570384493706170527562661658311968833727440431133732432933822461602573217025600540840893729518226237865509846565810192066911518030093370340498344293018423291724542348353094232605940162800644635131312574089135620405694882603832537043991184377003894238435037952132773371565971758518200338901093295016316119294348542840341834431351464504151907522191086945838570860740785465854936134367329432409661060346437097677121549489893206197450285766331107675095471743464309219832047474380362711538233025223528757701550176858426248427568315708109247244738953537198303103096683345086986435452120084396620434910999323244098253908369251444607790996774655487413591641058059947179415312050513816507821541150417209841078605358196580904753370145252606532025046560074592130737665707239217494015257127136253304807012153902996787690959310429618200688738434048369
Then just use the integer factorization website or yafu to factorize \(23(p-1)\), after that we can calculate the private key d using the Euler’s totient (phi)

Submit \(23(p-1)\) as the modulus at challenge server:
This is my new Oblivious transfer protocol built on top of the crypto primitive (factorisation is hard)
You should first generate a number h which you know the factorisation,
If you wish to know the first part of the key, send me h
If you wish to know the second part of the key, send me h - 23
Now what's your number: 1036005250634368665588082539989421470356810071500133575002975815339090040752757334257601033021464067631890495389238681622755597949322606480757099466715851545136017427988485090688093874231588836335239673071659838482606458892519050192840138460764719271304777124202190073389477913281431419037097557874505715093977619814735738606983833850314978000843863231068117742338232328776748727235799105724409264570384493706170527562661658311968833727440431133732432933822461602573217025600540840893729518226237865509846565810192066911518030093370340498344293018423291724542348353094232605940162800644635131312574089135620405694882603832537043991184377003894238435037952132773371565971758518200338901093295016316119294348542840341834431351464504151907522191086945838570860740785465854936134367329432409661060346437097677121549489893206197450285766331107675095471743464309219832047474380362711538233025223528757701550176858426248427568315708109247244738953537198303103096683345086986435452120084396620434910999323244098253908369251444607790996774655487413591641058059947179415312050513816507821541150417209841078605358196580904753370145252606532025046560074592130737665707239217494015257127136253304807012153902996787690959310429618200688738434048346
Now I send you these 2 numbers
pow(k1, e, N) = 227475657038456265943517904254041042003607783345391710569227323467226389575880201885989263427167060280605120992128646927236338098028640206489325185853292294927661352756239166215574784031195995610873972755884202116328668481769618026025274839682134248683568535707179768257074194771359446973574252519010388863036781732830442541652129422957796515980455596371037955107448972716696690802467208591252541657480824912284798872378603811231539491401429658019949080079231240436852804414525587855165662593254558044109188363181467025212426819815402274194480735927504878748597499921924824522147727786252658888991349324223371663944479018271990336414462431645025192068673909939876873829697455413663408237364336922328008886317898053363309736800289031982206068087268294724691953555716139559276786384463612599853593220947961613443071472982082169990020346425892652123914783297488113484559921075533630969595026846415316834271720690852667017284374749495993497104100917522849908556590508026999751142024715257019594567943436552938313325172377591859611774500959163001483306010868555787159006354687095273384354052442406161458973609316625228803316602696409814034315217536594184049621802582156545561969181208862764605964448523526093244898102377106852976824458607
pow(k2, e, N+23) = 27973436531703552514258017199148970681461059857319121641966059310000323546348290650143916192744821766856859500062813433980836391930227220158253675628332520825556907916863544584995870852573883643542421714287398611262014339373462798676805332156097698707885210957250367497578086593242735933948272125675806459832331993971623845134549934497914019400788963631057142525242791130596627948221881722487478966246091329410874180997928112081768911422374244707252612810897359481388277562434738235447701602130091390535846763773129292673007101388088639774837377994715289370568741454936805043498558105461948193682189559209385297766715540280390051741628954933961608749624169301272298278058092957782660993239121672718258824452302943541447799265810457101236142133811140579314980314481983421252417685128613460087304918173940064949740158001169665503478058439196613601391381211141229818221683006538556083891170630205781188192141298947381518385734144986878386085887533938990876921293982021421383039860562598215436375145923996418711495085099350752326757775481717336902685884978584286831208020426348041518404417863457242744747049311128183730787364738583085451113205578180081399215505442870581431056925744930168285768175967902006141860264961279196416672706702
Since you only know how to factorise one of them, you can only get one part of the data :D
This protocol is secure so sending this should not have any problem
flag = 05ee804bae05c337112a318192151435f628b82dafd200111dce7d073a612ba9864ae788abea8e082ab0dc3f4fa32b4b367ff68086fda70704388d7cce4b5e70ec
Bye bye!
Calculate both private keys, and decrypt the flag!!
import hashlib
from pwn import *
from Crypto.Util.number import long_to_bytes
c1 = 227475657038456265943517904254041042003607783345391710569227323467226389575880201885989263427167060280605120992128646927236338098028640206489325185853292294927661352756239166215574784031195995610873972755884202116328668481769618026025274839682134248683568535707179768257074194771359446973574252519010388863036781732830442541652129422957796515980455596371037955107448972716696690802467208591252541657480824912284798872378603811231539491401429658019949080079231240436852804414525587855165662593254558044109188363181467025212426819815402274194480735927504878748597499921924824522147727786252658888991349324223371663944479018271990336414462431645025192068673909939876873829697455413663408237364336922328008886317898053363309736800289031982206068087268294724691953555716139559276786384463612599853593220947961613443071472982082169990020346425892652123914783297488113484559921075533630969595026846415316834271720690852667017284374749495993497104100917522849908556590508026999751142024715257019594567943436552938313325172377591859611774500959163001483306010868555787159006354687095273384354052442406161458973609316625228803316602696409814034315217536594184049621802582156545561969181208862764605964448523526093244898102377106852976824458607
c2 = 27973436531703552514258017199148970681461059857319121641966059310000323546348290650143916192744821766856859500062813433980836391930227220158253675628332520825556907916863544584995870852573883643542421714287398611262014339373462798676805332156097698707885210957250367497578086593242735933948272125675806459832331993971623845134549934497914019400788963631057142525242791130596627948221881722487478966246091329410874180997928112081768911422374244707252612810897359481388277562434738235447701602130091390535846763773129292673007101388088639774837377994715289370568741454936805043498558105461948193682189559209385297766715540280390051741628954933961608749624169301272298278058092957782660993239121672718258824452302943541447799265810457101236142133811140579314980314481983421252417685128613460087304918173940064949740158001169665503478058439196613601391381211141229818221683006538556083891170630205781188192141298947381518385734144986878386085887533938990876921293982021421383039860562598215436375145923996418711495085099350752326757775481717336902685884978584286831208020426348041518404417863457242744747049311128183730787364738583085451113205578180081399215505442870581431056925744930168285768175967902006141860264961279196416672706702
n1 = 1036005250634368665588082539989421470356810071500133575002975815339090040752757334257601033021464067631890495389238681622755597949322606480757099466715851545136017427988485090688093874231588836335239673071659838482606458892519050192840138460764719271304777124202190073389477913281431419037097557874505715093977619814735738606983833850314978000843863231068117742338232328776748727235799105724409264570384493706170527562661658311968833727440431133732432933822461602573217025600540840893729518226237865509846565810192066911518030093370340498344293018423291724542348353094232605940162800644635131312574089135620405694882603832537043991184377003894238435037952132773371565971758518200338901093295016316119294348542840341834431351464504151907522191086945838570860740785465854936134367329432409661060346437097677121549489893206197450285766331107675095471743464309219832047474380362711538233025223528757701550176858426248427568315708109247244738953537198303103096683345086986435452120084396620434910999323244098253908369251444607790996774655487413591641058059947179415312050513816507821541150417209841078605358196580904753370145252606532025046560074592130737665707239217494015257127136253304807012153902996787690959310429618200688738434048346
n2 = n1+23
e = 0x10001
p = 45043706549320376764699240869105281319861307456527546739259818058221306119685101489460914479194089897038717190836464418380678171709678542641613020291993545440696409912542830029917124966590818971097377090072166890548106908370393486645223411337596490056729440182703916234325126664410061697265111211935031091042505209336336461173210167404999043514950575263831206188618796903336901184165178509756924546538456248094370763593985143998644944671323092770975344948802678372748566330458297430162152966358168065645502861312698561370349134494362630362795348627099640197493406656270982866963600028027614404894525614592191551951417557936393217008016391473662540653824005772755285477032979052188647873621522448526925841240993058340627450063674093561196617003780253850906988729802863258092798579540539550480884627699899005284760430139399889142859405700333699803119281056922601393368451320117892966653270588206856589138124279402105546448509048228141075606675530361004482464493264651584150092177582461758039608666228004271909059532671504686565077158934235373549611219997703452839654370165935122675702192052601786026319921590474119711745445765501392393328698895310032072422053879021478924222918967534991609224082738990769172143931722530464727758002103
# phi = (p-1)*(23-1)
d2 = pow(e,-1,(p-1)*(22))
k2 = pow(c2,d2,n2)
phi = 348512495312761557145035160493681489194440742833514809628451572665824338127436000938122522103774101301523351850961493677281457877987367784695494458188536065425337294163268386029204174312119724575365766099288242431369085717645755502019418555820430746139398986996796751466960039639411885529140929245883799462035396415218236091606784133064331770550081378524181260278648622540375861455189544968985552057444018088230969663397705139452994848417434672105410142745968725642345318907387312768976755568164856705825883503792576656696745914665543883498409890828836836115523210630186265787357242069674894757119765402634338788590071982483484043805615731082222770479197925118618391008374518381253398992944088719053200568587213760714988122725542129324361817967274436019027734703576852284447409385266781104709514522818629422177122130904957260856140689305992161174201765464320220097387852619684325663745592195839226248474770903242551558418804860942196936012745695879911538377945361785257956805046205491751651901910839972083678831121892359227585710665430700513406440537074946837186954678005556556889013935520260206882258019442734558785173383127902965244970926080000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000
d1 = pow(e,-1,phi)
k1 = pow(c1,d1,n1)
k = k1^k2
flag = bytes.fromhex("05ee804bae05c337112a318192151435f628b82dafd200111dce7d073a612ba9864ae788abea8e082ab0dc3f4fa32b4b367ff68086fda70704388d7cce4b5e70ec")
key = hashlib.shake_256(long_to_bytes(k)).digest(len(flag))
print(xor(flag,key))
# b'grey{waitttt_I_thought_factorization_is_hard!!?_bSug9kksE3W9SrPL}'
Thats it! It’s an interesting challenge
Flag
grey{waitttt_I_thought_factorization_is_hard!!?_bSug9kksE3W9SrPL}
Didn’t solve much during the CTF, but it’s was a nice ctf! Can check out their guthub repo: GreyCTF Challenge Github Repo