I participated TJCTF last weekend, and get 16th place!!
It was a nice and fun CTF, got easy one also got difficult one, here are some of the challenge writeups that I think are interesting
Challenges
sneaker-zipper
Attachment
It is a zip file, running unzip chall.zip can see it contains alot of txt file:
Archive: chall.zip
creating: flag/
...
...
...
inflating: flag/flag-070593ed-8a91-4c88-9581-0097b8fdc571.txt
inflating: flag/flag-46432104-1ea0-48df-97e7-8aa301053b0a.txt
inflating: flag/flag-93f6139d-4a0f-4bae-83fd-7f1453b7b4cc.txt
Then realize all txt file are the same and have the same text:
your flag is in another castle
So the flag must be hide in the zip file
Solving
Run zipinfo chall.zip and notice something odd:
Archive: chall.zip
Zip file size: 20965 bytes, number of entries: 101
drwxrwxr-x 2.0 unx 58 b- defN 22-Apr-24 17:40 flag/
?rw------- 2.0 unx 30 b- defN 22-Apr-24 17:40 flag/flag-01032e21-72c2-4a63-9d16-37df7ffc74ba.txt
?rw------- 2.0 unx 30 b- defN 22-Apr-24 17:40 flag/flag-f425a012-5abf-4d85-a635-20a2285877a7.txt
?rw------- 2.0 unx 30 b- defN 22-Apr-24 17:40 flag/flag-acdd6533-2055-4867-9c26-723126c17b76.txt
?rw------- 2.0 unx 30 b- defN 22-Apr-24 17:40 flag/flag-d1dd20df-860d-40d1-b4cc-59193927e9d3.txt
?rw------- 2.0 unx 30 b- defN 22-Apr-24 17:40 flag/flag-3db70f22-3c92-4d0b-a2c6-20428273f7eb.txt
?rw------- 2.0 unx 30 b- defN 22-Apr-24 17:40 flag/flag-952e430c-40f3-464f-b8ef-7c95c3753a72.txt
?rw------- 2.0 unx 30 b- defN 22-Apr-24 17:40 flag/flag-0ba9eb8c-42ef-4298-a92b-71a5569f22f0.txt
?rw------- 2.0 unx 30 b- defN 22-Apr-24 17:40 flag/flag-46eb486b-6348-4bc6-af11-f6f50543c4f9.txt
?rw------- 2.0 unx 30 b- defN 22-Apr-24 17:40 flag/flag-d11c6899-bc31-440f-810c-ef784ef819d6.txt
The size of the directory flag/ has larger size than other txt file…
Then I run zipdetails -v chall.zip, can see the flag/ contains compressed payload!!
0000 0004 50 4B 03 04 LOCAL HEADER #1 04034B50
0004 0001 14 Extract Zip Spec 14 '2.0'
0005 0001 00 Extract OS 00 'MS-DOS'
0006 0002 00 00 General Purpose Flag 0000
[Bits 1-2] 0 'Normal Compression'
0008 0002 08 00 Compression Method 0008 'Deflated'
000A 0004 04 8D 98 54 Last Mod Time 54988D04 'Sun Apr 24 17:40:08 2022'
000E 0004 99 CD 4D 14 CRC 144DCD99
0012 0004 39 00 00 00 Compressed Length 00000039
0016 0004 3A 00 00 00 Uncompressed Length 0000003A
001A 0002 05 00 Filename Length 0005
001C 0002 00 00 Extra Length 0000
001E 0005 66 6C 61 67 Filename 'flag/'
2F
0023 0039 2B C9 4A 2E PAYLOAD +.J.I...KM.N-
49 AB 2E CE *./.,....,(.q..R.32......-
4B 4D CC 4E .MR..M.......,Mk..
2D 2A 8E 2F
CF 2C C9 88
AF CA 2C 28
00 71 12 8B
52 E3 33 32
0B E2 F3 F2
ED E3 2D CC
4D 52 0C CD
4D 92 92 8C
CC D2 92 D3
2C 4D 6B B9
00
The payload is compressed using deflate, so we just need to inflate to get the content
We can do this using python script, found someone already implement the code here
My solution script:
import zlib
def inflate(data):
decompress = zlib.decompressobj(
-zlib.MAX_WBITS # see above
)
inflated = decompress.decompress(data)
inflated += decompress.flush()
return inflated
flag = bytes.fromhex("2BC94A2E49AB2ECE4B4DCC4E2D2A8E2FCF2CC988AFCA2C280071128B52E333320BE2F3F2EDE32DCC4D520CCD4D92928CCCD292D32C4D6BB900")
print(inflate(flag))
# b'tjctf{sneakers_with_zippers_are_hip_no?_874d174bb26fcf95}\n'
Also can decompress it using CyberChef if you like
factor-master
Attachment
Can guess it is about RSA factoring N? Look at the server source:
#!/usr/local/bin/python -u
from Crypto.Util.number import getPrime, isPrime, getRandomInteger
import sys, random
print("Are you truly the master here?")
print()
print("We'll have to find out...")
print()
def fail():
print("You are not the master!")
sys.exit(1)
def challenge1():
p = getPrime(44)
q = getPrime(1024)
n = p * q
return [p, q], n
def challenge2():
p = getPrime(1024)
q = p + getRandomInteger(524)
if q % 2 == 0: q += 1
while not isPrime(q): q += 2
n = p * q
return [p, q], n
def challenge3():
small_primes = [n for n in range(2,10000) if isPrime(n)]
def gen_smooth(N):
r = 2
while True:
p = random.choice(small_primes)
if (r * p).bit_length() > N:
return r
r *= p
p = 1
while not isPrime(p):
p = gen_smooth(1024) + 1
q = getPrime(1024)
n = p * q
return [p, q], n
challenges = [challenge1, challenge2, challenge3]
responses = ["Okay, not bad.", "Nice job.", "Wow."]
for i, chal in enumerate(challenges):
print(f"CHALLENGE {i+1}")
factors, n = chal()
factors.sort()
print(f"n = {n}")
guess = input("factors = ? ")
if guess != " ".join(map(str,factors)):
fail()
print(responses[i])
print()
print("Here's your flag:")
with open("flag.txt") as f:
print(f.read().strip())
Can see it got 3 challenge to pass, pass all to get the flag!
Challenge 1
First challenge was easy because p is small so normal factorize algorithm can do, this case I use primefac library
Challenge 2
Second challenge can see the almost half high bits of p and q are the same, therefore we can apply fermat factorization on this
Python implementation:
def fermat_factor(n):
assert n % 2 != 0
a = gmpy2.isqrt(n)
b2 = gmpy2.square(a) - n
while not gmpy2.is_square(b2):
a += 1
b2 = gmpy2.square(a) - n
p = a + gmpy2.isqrt(b2)
q = a - gmpy2.isqrt(b2)
return int(p), int(q)
Challenge 3
For last challenge it generate a smooth number as p-1
According to here, if p-1 or q-1 is smooth number then we can use Pollard’s p − 1 algorithm to factorize it
Python implementation:
def pollard(n):
a = 2
b = 2
while True:
a = pow(a, b, n)
d = gmpy2.gcd(a - 1, n)
if d > 1:
return int(d)
b += 1
Solving
Here is my python script to solve this, unfortunately didn’t save the flag and server is down 🙁
from primefac import primefac
import gmpy2
from pwn import *
def pollard(n):
a = 2
b = 2
while True:
a = pow(a, b, n)
d = gmpy2.gcd(a - 1, n)
if d > 1:
return int(d)
b += 1
def fermat_factor(n):
assert n % 2 != 0
a = gmpy2.isqrt(n)
b2 = gmpy2.square(a) - n
while not gmpy2.is_square(b2):
a += 1
b2 = gmpy2.square(a) - n
p = a + gmpy2.isqrt(b2)
q = a - gmpy2.isqrt(b2)
return int(p), int(q)
p = remote("tjc.tf", 31782)
# p = process(["python3","server.py"])
p.recvuntil("n = ")
n = int(p.recvuntil("\n")[:-1])
P,Q = list(primefac(n))
p.sendlineafter("? ",f"{P} {Q}")
p.recvuntil("n = ")
n = int(p.recvuntil("\n")[:-1])
P,Q = list(fermat_factor(n))
if Q>P:
p.sendlineafter("? ",f"{P} {Q}")
else:
p.sendlineafter("? ",f"{Q} {P}")
p.recvuntil("n = ")
n = int(p.recvuntil("\n")[:-1])
P = pollard(n)
Q = n//P
if Q>P:
p.sendlineafter("? ",f"{P} {Q}")
else:
p.sendlineafter("? ",f"{Q} {P}")
p.interactive()
morph-master
Attachment
Look at the source code, looks like a cryptosystem but I have no idea which one:
#!/usr/local/bin/python -u
from Crypto.Util.number import *
N = 1024
p = getPrime(N)
q = getPrime(N)
assert GCD(p * q, (p - 1) * (q - 1)) == 1
n = p * q
s = n ** 2
λ = (p - 1) * (q - 1) // GCD(p - 1, q - 1)
g = getRandomRange(1, s)
L = lambda x : (x - 1) // n
μ = pow(L(pow(g, λ, s)), -1, n)
def encrypt(m):
r = getRandomRange(1, n)
c = (pow(g, m, s) * pow(r, n, s)) % (s)
return c
def decrypt(c):
m = (L(pow(c, λ, s)) * μ) % n
return m
print(f"public key (n, g) = ({n}, ?)")
print(f"E(4) = {encrypt(4)}")
print()
print("Encrypt 'Please give me the flag' for your flag:")
c = int(input())
m = decrypt(c)
if long_to_bytes(m) == b"Please give me the flag":
print("Okay!")
with open("flag.txt") as f:
print(f.read())
else:
print("Hmm... not quite.")
The challenge description says:
My friend Pascal made this new cryptosystem
So lets search for Pascal cryptosystem, then found this wiki page, it looks exactly the same!
Homomorphic properties
As the wiki page says, we need n,g to encrypt messages
But now the challenge need us to encrypt Please give me the flag with just n.. but how??
We need to use the Homomorphic properties stated in wiki page:

Using the \(E(4)\) provided, we need to somehow calculate the ciphertext of Please give me the flag \(E(7703...503)\)
Let’s take alook at the last property: \(D(E(m_{1},r_{1})^{k} \mod{n^{2}})=km_{1}\mod n\)
But our target number is odd number, so impossible to find an integer \(k\) that \(4k=7703...503\)
But what if we calculate the inverse modular of it?
\[D(E(4)^{-1}\mod n^2) = -4 \mod n\] \[= n-4\]
As you can see, it decrypted into \(-4 \mod n\) also \(n-4\), so if n minus our target number is multipler of 4 then we can calculate the ciphertext using this method!!
For example if x is our target number: \[x = 7703…503\] If \(n-x \mod 4 =0\) then we let \(k=-\frac{n-x}{4}\):
\[D(E(4)^{-\frac{n-x}{4}} \mod n^2) = -\frac{n-x}{4}(4) \mod n\] \[= n+x \mod n\] \[\equiv x \mod n\]
As you can see, it will decrypt into our target number so let’s try it!!
Solving
Run the server.py
public key (n, g) = (13414246997667707727735219693453810593940548612833405932173217718480320338245468012091675869706946862678254873616044431603904294572073377864973604750895805793314090801704740289096480242796743783407979950634587810299454233203444803698205241954143947640432985388358783559312195653156408217460195734724494704832089872300370755039494862383513250875774555907452761497098967418675998436742480209238896984777386560243791509575672980161820589281892592431491582110762330599210595019804437458291764128892275264503988478479106506985442878884862775796207267235005464498763156122841407660131140950462563812093140730181658884417391, ?)
E(4) = 32949792533053951081448863524692440620820181800590533428150898044931933408443439707701674902358316081898792589607147214780843007558887037326207422826310517080173141208670099918456236917222778272991847708658467036071819888210814281232460415058374884906565253768054598372412691078480690931312274835829494436686111411568496316788577925197487853863211017323352211759369466996063801984284983328721982973675914823463822220765898770136108430556338313820660419668108646991342299164780746935794536468157991804533499234276740374046075849767795491795864280841585401589057251121502904995195331441625496397596671591523043306227840840417728505021492244212781131284844273765032415520393853895951850374974412365005730135421214191244512191973204337551689392824874707946592729720719984379555250886269719157336984807959651655299426652151510363186573584654597608598958562559957066392841738685943627007300395691164925155506585525618944246906429901156291850144022915046650207270597269145986812370843961268800533507457326275124725220575393045168637132883551768210319872172433721245699906057298012734590856502141535408999187442027752719088125757398376238744356731393116342826656068417050967541284325696464030401902269413201306479357582100233483607403990886
Encrypt 'Please give me the flag' for your flag:
Copy the n and e into the script below:
from Crypto.Util.number import *
n = ?
e = ?
target = bytes_to_long(b"Please give me the flag")
assert (n-target)%4==0
x = (n-target)//4
result = pow(e,-x, n**2)
print(result)
Unfortunately, the server is down so you can run the server.py yourself to test
If you got lucky it will print the result and you just paste the answer and you are done!
mac-master
Attachments
Look at the source:
KEY = os.urandom(16)
...
...
def nmac(message):
return hashlib.md5(message + KEY).hexdigest()
def query():
print("What message would you like to query a tag for?")
print("Enter message hex-encoded:")
hex_message = input()
message = bytes.fromhex(hex_message)
QUERIED.add(message)
print("Tag:", nmac(message))
def challenge():
print("Challenge time!")
print("Enter message hex-encoded:")
hex_message = input()
tag = input("Tag: ")
message = bytes.fromhex(hex_message)
if message in QUERIED:
print("You already queried that message!")
elif nmac(message) == tag:
print("Nice job!")
print("Flag:", FLAG)
As you can see, we need to somehow find the correct tag for the challenge message by querying any messages but not the challenge message
We know that MD5 is vulnerable to hash length extension attack, but it uses \(H(m||k)\) instead of \(H(k||m)\) so is not vulnerable
Hash collision
By searching h(m||k) found this page, saying we should find collisions of hash
In the wikipedia page of MD5 stated:
MD5 uses the Merkle–Damgård construction, so if two prefixes with the same hash can be constructed, a common suffix can be added to both to make the collision more likely to be accepted as valid data by the application using it.
So if we find collisions of A and B:
\[H(A)=H(B)\]
If both concatenate C the collision still remains
\[H(A||C)=H(B||C)\]
Solving
Therefore, we can solve this by using two messages that are the same MD5 hash (collision)
We pass the first message and get the MD5 hash, then we pass the second message and give the same first message hash
We can use the messages from wikipedia:
d131dd02c5e6eec4693d9a0698aff95c2fcab58712467eab4004583eb8fb7f8955ad340609f4b30283e488832571415a085125e8f7cdc99fd91dbdf280373c5bd8823e3156348f5bae6dacd436c919c6dd53e2b487da03fd02396306d248cda0e99f33420f577ee8ce54b67080a80d1ec69821bcb6a8839396f9652b6ff72a70
d131dd02c5e6eec4693d9a0698aff95c2fcab50712467eab4004583eb8fb7f8955ad340609f4b30283e4888325f1415a085125e8f7cdc99fd91dbd7280373c5bd8823e3156348f5bae6dacd436c919c6dd53e23487da03fd02396306d248cda0e99f33420f577ee8ce54b67080280d1ec69821bcb6a8839396f965ab6ff72a70
Test run server.py (need python 3.10):
Introducing Neil-MAC (NMAC), the future of hash-based message
authentication codes!
No longer susceptible to those pesky length extension attacks!
What do you want to do?
1) Query a message
2) Challenge
1
What message would you like to query a tag for?
Enter message hex-encoded:
d131dd02c5e6eec4693d9a0698aff95c2fcab58712467eab4004583eb8fb7f8955ad340609f4b30283e488832571415a085125e8f7cdc99fd91dbdf280373c5bd8823e3156348f5bae6dacd436c919c6dd53e2b487da03fd02396306d248cda0e99f33420f577ee8ce54b67080a80d1ec69821bcb6a8839396f9652b6ff72a70
Tag: 9e592577ba1c366fee963d78aaa39ec0
What do you want to do?
1) Query a message
2) Challenge
2
Challenge time!
Enter message hex-encoded:
d131dd02c5e6eec4693d9a0698aff95c2fcab50712467eab4004583eb8fb7f8955ad340609f4b30283e4888325f1415a085125e8f7cdc99fd91dbd7280373c5bd8823e3156348f5bae6dacd436c919c6dd53e23487da03fd02396306d248cda0e99f33420f577ee8ce54b67080280d1ec69821bcb6a8839396f965ab6ff72a70
Tag: 9e592577ba1c366fee963d78aaa39ec0
Nice job!
Flag: SKR{flag}
Yeah!! We made it! Then use the same method at the real server (Actually I didn’t solve it during the competition but still fun to explore it after)
mmocc
Attachment
Open the website given, we can click the cookie button and the number will increase
Look at the source code, notice we need to get infinity clicks to get the flag (Obviously impossible):
clicks: async (_req, res) => {
if (state.clicks === Infinity) res.json({ flag, ...state });
else res.json(state);
}
Solving
The static function is odd:
static: async (req, res) => {
const regex = /\.\.\//g;
const clean = (path) => {
const replaced = path.replace('../', '');
if (regex.test(path)) {
return clean(replaced);
}
return replaced;
};
const location = [__dirname, 'static', clean(req.url)];
if (location[2].endsWith('/')) location.push('index.html');
const file = path.join(...location);
let data;
try {
data = await fs.promises.readFile(file);
} catch (e) {
if (e.code === 'ENOENT') {
res.statusCode = 404;
res.end('not found');
return;
}
throw e;
}
const type = types.get(path.extname(file)) ?? 'text/plain';
res.setHeader('content-type', type);
res.end(data);
}
It will read file directory from server, but it checks for directory travesal
const regex = /\.\.\//g;
const clean = (path) => {
const replaced = path.replace('../', '');
if (regex.test(path)) {
return clean(replaced);
}
return replaced;
};
Notice it just replace the ../ once so is easy to bypass this with ..././
Because replacing ..././ will become ../
We just need to perform GET request to /..././..././flag.txt
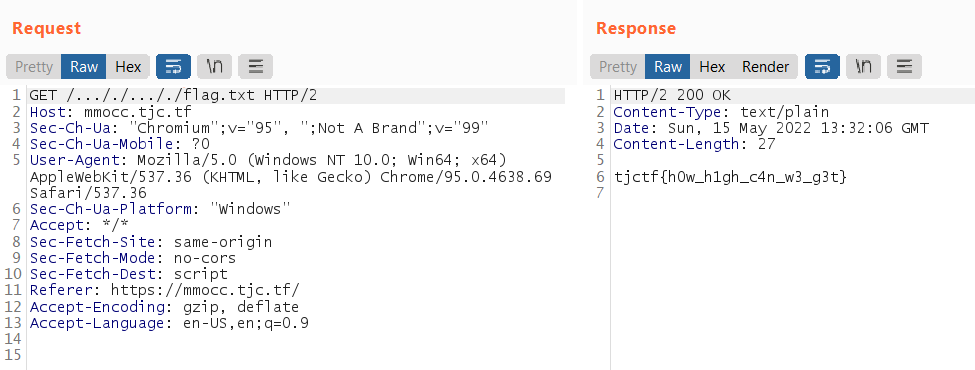
Conclusion
It was a nice CTF, I learned many things from it thanks to TJCSC!