I play this CTF last weekend, it was quite hard for me, end up only solve one challenge
Here are some of my writeups
Challenges
oh-my-grafana
Unfortunally, the challenge website is down now and no screenshot..
Basically it was using old version Grafana 2.6.0, by searching grafana exploit you can find it is vulnerable to Directory Traversal and Arbitrary File Read (CVE-2021-43798)
Here got some example of how to exploit it
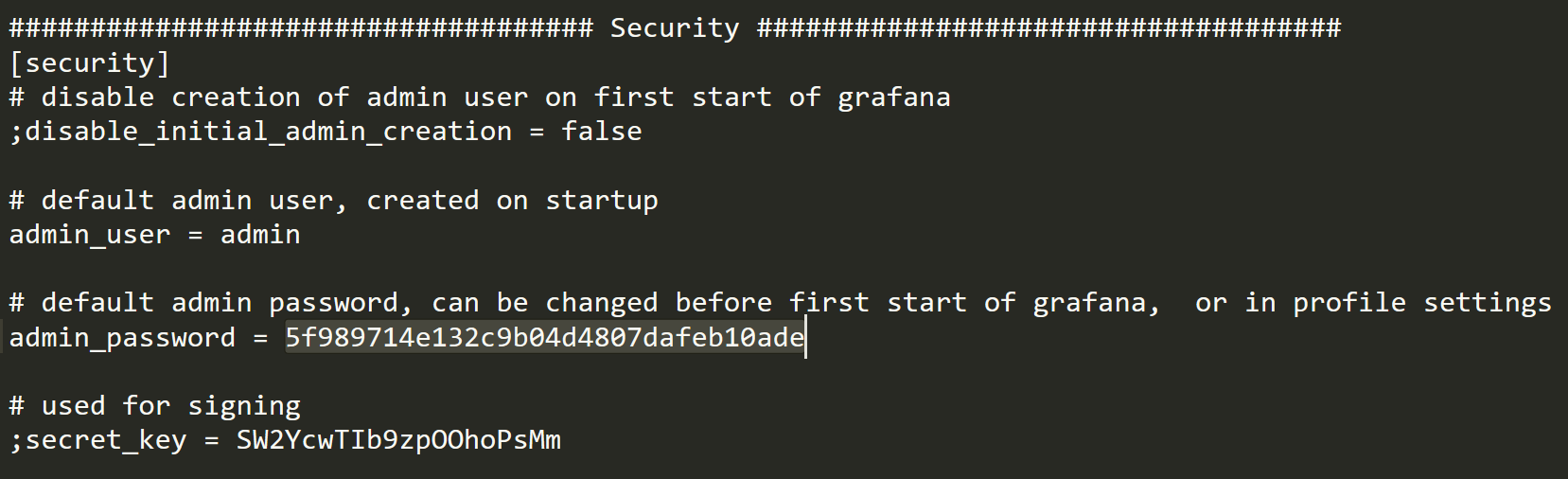
And I get the configuration file from /etc/grafana/grafana.ini, then found the admin credentials:
Then I tried to guess the flag file using the directory traversal bug but no luck..
After that I try to login into admin’s account see if anything I can do, then notice we can add database source
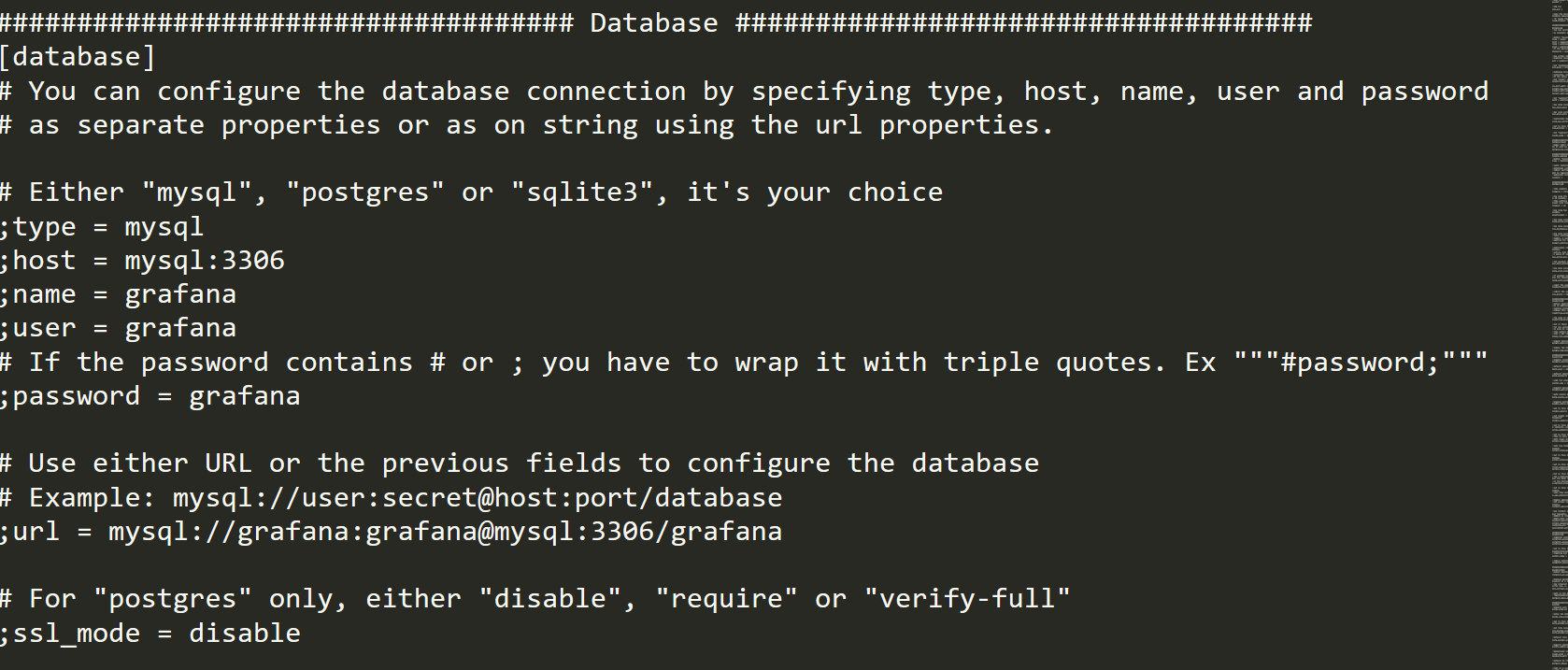
Remember the configuration file got the database credentails:
Therefore, I tried to add the mysql source using the credentails then I get the flag by querying the database table!
The query is something like select flag from fffffflllllllllaaaagggggg
Flag
*ctf{Upgrade_your_grafAna_now!}
ezRSA
Challenge file
from Crypto.Util.number import getStrongPrime
from gmpy import next_prime
from random import getrandbits
from flag import flag
p=getStrongPrime(1024)
q=next_prime(p^((1<<900)-1)^getrandbits(300))
n=p*q
e=65537
m=int(flag.encode('hex'),16)
assert m<n
c=pow(m,e,n)
print(hex(n))
#0xe78ab40c343d4985c1de167e80ba2657c7ee8c2e26d88e0026b68fe400224a3bd7e2a7103c3b01ea4d171f5cf68c8f00a64304630e07341cde0bc74ef5c88dcbb9822765df53182e3f57153b5f93ff857d496c6561c3ddbe0ce6ff64ba11d4edfc18a0350c3d0e1f8bd11b3560a111d3a3178ed4a28579c4f1e0dc17cb02c3ac38a66a230ba9a2f741f9168641c8ce28a3a8c33d523553864f014752a04737e555213f253a72f158893f80e631de2f55d1d0b2b654fc7fa4d5b3d95617e8253573967de68f6178f78bb7c4788a3a1e9778cbfc7c7fa8beffe24276b9ad85b11eed01b872b74cdc44959059c67c18b0b7a1d57512319a5e84a9a0735fa536f1b3
print(hex(c))
#0xd7f6c90512bc9494370c3955ff3136bb245a6d1095e43d8636f66f11db525f2063b14b2a4363a96e6eb1bea1e9b2cc62b0cae7659f18f2b8e41fca557281a1e859e8e6b35bd114655b6bf5e454753653309a794fa52ff2e79433ca4bbeb1ab9a78ec49f49ebee2636abd9dd9b80306ae1b87a86c8012211bda88e6e14c58805feb6721a01481d1a7031eb3333375a81858ff3b58d8837c188ffcb982a631e1a7a603b947a6984bd78516c71cfc737aaba479688d56df2c0952deaf496a4eb3f603a46a90efbe9e82a6aef8cfb23e5fcb938c9049b227b7f15c878bd99b61b6c56db7dfff43cd457429d5dcdb5fe314f1cdf317d0c5202bad6a9770076e9b25b1
As you can see, the generation of the prime factors are not secure because p and q top 124bits are the same, and middle 600bits q is the oppsite of p
For example: if p=1101 then q=0010
Top bits
The top 124bits can be recover by get squre root of n because the top 124bits of p and q are the same so we can square root 248bits of n to get the top 124bits of both factors
Solution:
import gmpy2
n = 0xe78ab40c343d4985c1de167e80ba2657c7ee8c2e26d88e0026b68fe400224a3bd7e2a7103c3b01ea4d171f5cf68c8f00a64304630e07341cde0bc74ef5c88dcbb9822765df53182e3f57153b5f93ff857d496c6561c3ddbe0ce6ff64ba11d4edfc18a0350c3d0e1f8bd11b3560a111d3a3178ed4a28579c4f1e0dc17cb02c3ac38a66a230ba9a2f741f9168641c8ce28a3a8c33d523553864f014752a04737e555213f253a72f158893f80e631de2f55d1d0b2b654fc7fa4d5b3d95617e8253573967de68f6178f78bb7c4788a3a1e9778cbfc7c7fa8beffe24276b9ad85b11eed01b872b74cdc44959059c67c18b0b7a1d57512319a5e84a9a0735fa536f1b3
top_bits = int(gmpy2.iroot(n>>(2048-248),2)[0])
print(hex(top_bits))
# 0xf376c68d76f4ab9b4d247852ef07159
Middle Bits
I stuck on this part, found something like recover from XOR both factors but it require the least significant bits..
This one is tough, I didn’t solve it during the CTF, I end up looking at the official writeup I think I will never think of it..
The idea is to brute force the bits order of p & q one by one, because both bits must be oppsite (01 or 10), if product of them is < n then is the correct order else is wrong
import gmpy2
n = 0xe78ab40c343d4985c1de167e80ba2657c7ee8c2e26d88e0026b68fe400224a3bd7e2a7103c3b01ea4d171f5cf68c8f00a64304630e07341cde0bc74ef5c88dcbb9822765df53182e3f57153b5f93ff857d496c6561c3ddbe0ce6ff64ba11d4edfc18a0350c3d0e1f8bd11b3560a111d3a3178ed4a28579c4f1e0dc17cb02c3ac38a66a230ba9a2f741f9168641c8ce28a3a8c33d523553864f014752a04737e555213f253a72f158893f80e631de2f55d1d0b2b654fc7fa4d5b3d95617e8253573967de68f6178f78bb7c4788a3a1e9778cbfc7c7fa8beffe24276b9ad85b11eed01b872b74cdc44959059c67c18b0b7a1d57512319a5e84a9a0735fa536f1b3
top_bits = int(gmpy2.iroot(n>>(2048-248),2)[0])
# Put all 1 in p and 0 in q
p = top_bits<<900 | (2**900 - 1)
q = top_bits<<900
# Start from 125th bits (1024-125)
for i in range(899, 301, -1):
cur = 1<<i
# Swap p to 0 and q to 1
# if less than n then is correct order
# else no changes
if (p^cur) * (q^cur) < n:
p ^= cur
q ^= cur
print(hex(p))
print(hex(q))
# 0xf376c68d76f4ab9b4d247852ef07159a09eeac920ac89148a8dee4f3c359a291b6bf03ab9258ca64783c416fcfeade13cf3c18a7677c29283c7fc6bfcdbba1d6fecbe9e243cc2e3ef0fe60035e1dbc727f3522bfab2bc28d5e29bfffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
# 0xf376c68d76f4ab9b4d247852ef071595f611536df5376eb757211b0c3ca65d6e4940fc546da7359b87c3be90301521ec30c3e7589883d6d7c380394032445e290134161dbc33d1c10f019ffca1e2438d80cadd4054d43d72a1d64000000000000000000000000000000000000000000000000000000000000000000000000000
As you can see, we get the middle bits too!
Remaining Bits
If we know the high bits of the factor, we can find the remaining bits using coppersmith method, according to this book Recovering cryptographic keys from partial information
By searching rsa known high bits ctf, got many sage script implemented this attack
You can also use the script from the offical writeup
Then I wrote a sage script to find the remaining bits then decrypt the flag:
from Crypto.Util.number import *
n = 0xe78ab40c343d4985c1de167e80ba2657c7ee8c2e26d88e0026b68fe400224a3bd7e2a7103c3b01ea4d171f5cf68c8f00a64304630e07341cde0bc74ef5c88dcbb9822765df53182e3f57153b5f93ff857d496c6561c3ddbe0ce6ff64ba11d4edfc18a0350c3d0e1f8bd11b3560a111d3a3178ed4a28579c4f1e0dc17cb02c3ac38a66a230ba9a2f741f9168641c8ce28a3a8c33d523553864f014752a04737e555213f253a72f158893f80e631de2f55d1d0b2b654fc7fa4d5b3d95617e8253573967de68f6178f78bb7c4788a3a1e9778cbfc7c7fa8beffe24276b9ad85b11eed01b872b74cdc44959059c67c18b0b7a1d57512319a5e84a9a0735fa536f1b3
p = 0xf376c68d76f4ab9b4d247852ef07159a09eeac920ac89148a8dee4f3c359a291b6bf03ab9258ca64783c416fcfeade13cf3c18a7677c29283c7fc6bfcdbba1d6fecbe9e243cc2e3ef0fe60035e1dbc727f3522bfab2bc28d5e29bfffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffffff
c = 0xd7f6c90512bc9494370c3955ff3136bb245a6d1095e43d8636f66f11db525f2063b14b2a4363a96e6eb1bea1e9b2cc62b0cae7659f18f2b8e41fca557281a1e859e8e6b35bd114655b6bf5e454753653309a794fa52ff2e79433ca4bbeb1ab9a78ec49f49ebee2636abd9dd9b80306ae1b87a86c8012211bda88e6e14c58805feb6721a01481d1a7031eb3333375a81858ff3b58d8837c188ffcb982a631e1a7a603b947a6984bd78516c71cfc737aaba479688d56df2c0952deaf496a4eb3f603a46a90efbe9e82a6aef8cfb23e5fcb938c9049b227b7f15c878bd99b61b6c56db7dfff43cd457429d5dcdb5fe314f1cdf317d0c5202bad6a9770076e9b25b1
PR.<x> = PolynomialRing(Zmod(n))
f=x+p
roots=f.small_roots(X=2**430,beta=0.4)
p=int(p+roots[0])
assert n%p==0
q = n//p
phi = (p-1)*(q-1)
d = inverse(65537, phi)
print(long_to_bytes(pow(c,d,n)))
# b'*CTF{St.Diana_pls_take_me_with_you!}'
Flag
*CTF{St.Diana_pls_take_me_with_you!}